Objective:
Apply the method of integration by substitution to the resolution of definite integrals
Method (Recall)
The method by substitution consists in substituting the given variable by another variable
that makes the integral easier to calculate.
Let’s integrate 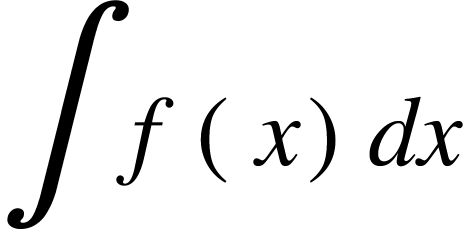 by substitution.
by substitution.
If this integral can be written 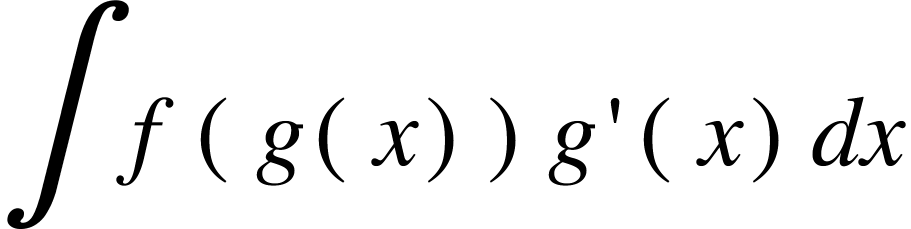 with
with 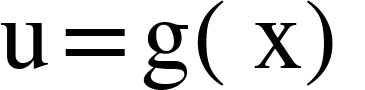 and
and 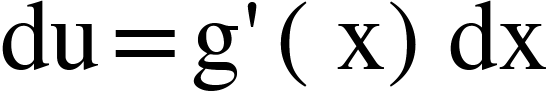 then
then
The integral 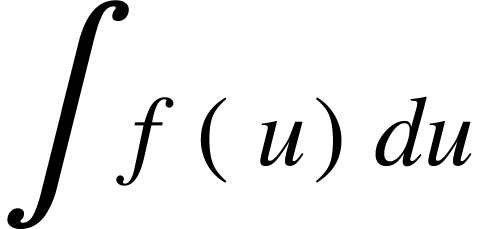 becomes easier to calculate. In the case of a definite integral
becomes easier to calculate. In the case of a definite integral
we have to calculate the new limits of integration for u.
Example I
Let’s calculate 
= 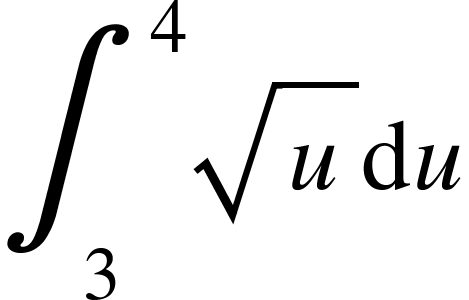
= 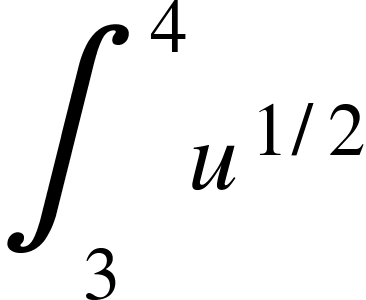
= 
= 
= 
=
Example II Evaluate 
We can rewrite the expression as:
We have here 2 separate expressions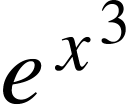 and x²
and x²
We seek to find out if the expression x² closed to dx is the derivative of the expression x³ in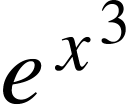 .
.
We notice that x² is almost the derivative of x³ . It misses the term 3. Therefore we have
to multiply and divide by 3 in order to have 3 x² . The given expression becomes:
We can rewrite the expression as:
We have here 2 separate expressions
We seek to find out if the expression x² closed to dx is the derivative of the expression x³ in
We notice that x² is almost the derivative of x³ . It misses the term 3. Therefore we have
to multiply and divide by 3 in order to have 3 x² . The given expression becomes:

We can write
Then we have:
If we do a change of variable by writing u = x³ du/dx = 3x² du = 3x²dx.= g'(x)dx
f(g(x)) =
In the expresion u = x³, for x = 0 u = 0, for x = 2 u = (2)³ = 8
Let's substitute f(g(x)) by f(u) and g'(x)dx by du:
Let's substitute f(u) by

N.B. We have solved the second example by writing the given function as a composite function. We can skip these steps by doing the change of variable right away.as it was done in the first example,
Practice




No comments:
Post a Comment