Integrating the product of the power of sine by the power of cosine

Integrating a function of the product of sine by cosine: f(x) = sin^mxcos^nx ( read sine  exponent m x by cos exponent n x)

Method

1. If m is odd let u = cosx
2. If n is odd let u = sinx
3. If m and n are even use identities to reduce the power of sine and cosine

Example I

Solve ∫sin³xcos⁴xdx

 Since m is odd let u = cox then du =- sinxdx  dx = -du/sinx

Let's substitute cox and dx in the integral

∫sin³xcos⁴xdx = ∫sin³xu⁴.-du/sinx

Let's simplify by sinx:

∫sin³xcos⁴xdx = - ∫sin²xu⁴du

In order to have the integral as a function of u let's express sin²x as an expression of cosx

sin²x = 1-cos²x = 1-u²

Let's substitute sin²x

∫sin³xcos⁴xdx = -∫(1-u²)u⁴du

                     = -∫(u⁴-u⁶)du

                     = -(u⁵/5-u⁷/7 +C

                     = -u⁵/5-u⁷/7 +C

                     =  -cos⁵x/5-cos⁷x/7 +C ( by substituting u by cosx)

Example II

Solve ∫sin²xcos²xdx.

We have m and n even. We use identities to reduce power.

 sin²xcos²xdx. = (1 - cos2x)/2.(1 + cos2x)/2 = 1 - cos²2x/4 = sin²2x/4

Let's reduce the power of sin²2x

 sin²2x = (1 - cos4x)/2

 sin²2x/4 = (1 - cos4x)/8 = 1/8 - 1/8cos4x

 ∫sin²xcos²xdx = ∫(1/8 - 1/8cos4x)dx

                      =1/8 ∫dx - 1/8 ∫cos4xdx

                      = 1/8x - 1/8sin4x + C

Practice

Solve

1) ∫sin⁴xcos³x
2) ∫sin⁴xcos⁴x
.

Integration of trigonometric functions involving the power of sine or the power of cosine

Objective:

To compute the integral of a function involving the power of sine or the power of cosine

Method

In order to solve the integral of the power of sine or the power of cosine we have to reduce their power. We use the following formulas:

sin²x  = 1/2 (1-cos2x )
cos²x = 1/2 ( 1 + cos2x )

Example I

Solve   ∫ sin²xdx

Let's substitute sin²x by  1/2 ( 1-cos2x )

∫sin²xdx = ∫ [1/2 ( 1-cos2x )] dx
         
            = 1/2 ∫ ( 1-cos2x ) dx
         
            = 1/2 [ ∫ dx - ∫ cos2x dx ]

 Let's solve ∫ cos2x dx

Let's use the substitution method by writing u = 2x

Then du = 2xdx dx = du/2

∫ cos2x dx =  ∫ cosu.du/2
                = 1/2 ∫ cosudu

                = 1/2 sinu + C

                =  1/2 sin2x + C

Let's solve the expression between brackets:

 ∫sin²xdx = 1/2 ( x - 1/2 sin2x ) + C

             =  1/2 x - 1/4 sin2x + C
  
Example II   Evaluate ∫ cos⁴x

The technique used to solve  the integral of the power of cosine and the power of sine consists in reducing the power of these functions.

Let's first reduce the power of cos⁴x
cos⁴x = ( cos²x )²

Let's reduce the power of cos²x by using the formula cos²x = 1/2 ( 1 + cos2x )

cos⁴x = [ 1/2 ( 1 + cos2x ) ]²

         = 1/4 ( 1 + 2cos2x + cos²2x )

         = 1/4 + 1/2cos2x + 1/4cos²2x

Let's reduce the power of cos²2x:

cos²x = 1/2 ( 1 + cos2x ). By analogy  cos²2x = 1/2 ( 1 + cos4x ). Then 1/4cos²2x = 1/8 + 1/8cos4x

Therefore cos⁴x = 1/4 + 1/2cos2x + 1/8 + 1/8cos4x

                 cos⁴x = 3/8 + 1/2cos2x + 1/8cos4x
               
∫cos⁴xdx = ∫( 3/8 + 1/2cos2x + 1/8cos4x )dx
             
              = 3/8∫dx + 1/2∫ cos2xdx + 1/8∫ cos4xdx
           
In the example above we found ∫cos2xdx = 1/2 sin2x + C. By analogy ∫cos4xdx = 1/4 sin4x + C

  ∫cos⁴xdx = 3/8x + 1/2 ( 1/2 sin2x ) + 1/8 ( 1/4 sin4x ) + C 
             
                 = 3/8x + 1/4 sin2x  + 1/32 sin4x  + C

Practice 

Evaluate:

1) ∫cos²xdx
2) ∫sin⁴xdx

Interested in learning more about Calculus visit Center for Integral Development

For contact about tutoring and private lessons visit New Direction Education Services

Application of the integration by substitution to trigonometry integrals

The integration by substitution method can be used to find the integral of some trigonometric expressions. Here are the basic trigonometric formulas that can be used with the substitution method.
The change of variable u can be applied as long as it is a differentiable function of x

Example I

Solution

The argument of the cosine function is 3x + 2, Let's make u = 3x + 2. then du = 3 dx  dx = 1/3du
Let;s substitute dx in the given expression:

                ∫ cos(3x + 2) dx = ∫cosu.1/3du

                                          = 1/3∫ cosudu

                                          = 1/3sinu + C

                                            = 1/3sin (3x +2) + C

Example II

Solution

Example III

Solution

Let's substitute tanx by sinx/cosx in the expression:

∫tanxdx = ∫ cosx/sinxdx

Let's u = sinx. Then du = cosxdx or dx = du/cosx

Let's substitute u and dx in the given expression

∫cosx/sinxdx = ∫cosx/u.du/cosx

Let's simplify by cosx:

∫cosx/sinxdx = ∫du/u = lnu + C = ln sinx + C

Practice

Evaluate:

1) ∫sin(4x + 1)dx

2) ∫1/sin²xdx

3) ∫cotx

Interested about learning more about integration visit Center for Integral Development

A guide to find the integral of a rational function by decomposing it in partial fractions

The calculation of the integral of some functions implies the use of some ingenious techniques. In this post I am going to expose a method to find the integral of a rational function. It consists in decomposing the rational function into partial functions easier to integrate. This method is called "integration by partial decomposition".

In order to apply the techniques we make the following considerations:

1. The degree of the numerator must be one degree less than that of the denominator
2. The denominator must be decomposed into a product of factors. The number of factors will determine the number of partial fractions. Example: the function 2x + 3/(x+1)(x+2) can be decomposed as the sum of A/x+1 + B/x+2.
3. If the denominator is not decomposed into a product of factors it has to be so. Example: the function f(x) =  3x + 1/x² + 5x + 6 cannot be decomposed unless we factor it in a product of factors. Factoring the denominator as (x+2)(x+3) the function can be decomposed as: 3x + 1/(x+2)(x+3) = A/x+2 + B/x+3
4.  If the denominator is a power like (x + a)ⁿ then a rational function like N/(x + a)ⁿ can be written as: N/(x + a)ⁿ = A₁/x + a + A₂/(x+a)² + A₃/(x + a)³+.....An/(x+a)ⁿ

Example 1  Find the integral of the function f(x) = 2x+3/(x+1)(x+2)

The denominator is decomposed into 2 factors.  The fraction can be decomposed  into 2 partial fractions as follows:

2x+3/(x+1)(x+2) = A/x+1 + B/x+2

The goal here is to determine A and B. In order to do that, we have to go through a number of steps

1) Making the equality above identically equal. That will happen when the denominator of the fraction on the second side of the equation is equal to to the denominator of the fraction on the first side of the equation. The numerator of the fraction on the second side is written in the same way as the numerator of the fraction on the first side of the equation
2) Set a system of 2 equations containing A and B in order to determine these unknown
3) Substitute A and B in the expression: 2x+3/(x+1)(x+2) = A/x+1 + B/x+2

Let's do step 1:

2x+3/(x+1)(x+2) = A(x+2) + B(x + 1)/ (x+1)(x+2)

2x+3/(x+1)(x+2) = Ax + 2A + Bx + B/ (x + 1) (x + 2)

 2x+3/(x+1)(x+2) = (A + B)x + 2A + B/(x + 1) (x + 2

Let's simplify by (x + 1) (x + 2):

2x + 3 = (A + B)x + 2A + B

Now we can go to step 2:

By identification we have: A + B = 2 (1)  3 (2) 2A + B = 3

Let's solve this system of the 2 equarions by multiplying the first equarion by -2 and adding the new equation to the second equation

-2A-2 B = -4
2A + B = 3

We then obtain: -B = -1 B = 1

Let's substitute B in the second equation
:2A + 1 = 3
2A = 2  A = 1

Let's go to the final step 3:

Let's substitute A and B in the expression developed above:

2x + 3/(x+1)(x+2) = 1/x + 1 + 1/x+2

Now we can calculate the integral of 2x + 3/ (x + 1) (x + 2):

∫ (2x + 3/(x+1)(x+2) = ∫(1/x + 1 + 1/x + 2)dx

                                = ∫1/x + 1dx +  ∫1/x + 2 dx

                                = ln❘x + 1❘ + ln❘x + 2❘ + C

Example 2. Find the integral of the function f(x) =  3x + 1/x² + 5x + 6

Let's factor the denominator: x² + 5x + 6 = (x + 2) (x + 3)

Now the function can be written as:  f(x) =  3x + 1/ (x + 2) (x + 3)

Let's decompose the function in partial fractions:

3x + 1/ (x + 2) (x + 3) = A/x + 2 + B/x + 3

Step 1

In order to determine A and B let's do the first step which consists in making the expression above identically equal:

3x + 1/ (x + 2) (x + 3) = A(x + 3) + B(x + 2)/ (x + 2) (x + 3)

The equality of these two fractions implies the equality of the denominators and that of the numerators. The denominators being equal, let's equalize the numerators.

3x + 1 = A(x + 3) + B(x + 2)

3x + 1 = Ax + 3A + Bx + 2B

  3x + 1 = (A + B)x + 3A + 2B

Now we go to step 2. The equality is true if the coefficients of x and the constant terms are equal:

Step 2

A + B = 3 (1)  3A + 2B = 1 (2)

Let's multiply the first equation by -3 and add the new equation to the second equation
-3A - 3B = -6 (3)
  3A + 2B = 1 (2)

B = -5

Let's substitute B in the first equation

A-5 = 3 A = 8

Step 3

Let's substitute A and B in the decomposed function above:

    3x + 1/ (x + 2) (x + 3) = 8/x + 3 - 5/x + 2

Let's integrate both sides
:
∫3x + 1/ (x + 2) (x + 3)dx = ∫(8/x + 3 - 5/x + 2)dx =  ∫8/x + 3dx - ∫5/x + 2)dx = 8∫1/x + 3dx -5∫1/x + 2dx = 8ln❘x + 3❘-5ln❘x + 2❘ + C

From the example above we can set the general rule:

1) Decompose the rational function into an expression containing unknowns to determine: A, B, C, etc.
2) Make the equation identically equal
3) Set a system of equations that allow to determine the unknowns
4) When the unknowns are determined. substitute them in the function theoretically decomposed.
5) Calculate the integral 

Practice: Integrate the function: f(x) = 2x-3/(3x + 1)²

Interested about learning more about integration visit Center for Integral Development

The art of mastering the integration by parts

The integration parts allows to calculate the integral of the product of some functions. Let's derive a formula for it:

The formula for the derivative of a product is (uv)' = u'v + uv'

Then uv' = (uv)'-u'v

Let's integrate the 2 sides;

∫uv'dx = ∫(uv)'dx-∫u'vdx

∫u.(dv/dx).dx = uv-∫(du/dx).vdx

Let's simplify:

∫udv = uv-∫vdu

Example 1. Evaluate ∫xsinxdx;

Let's apply the formula: ∫udv = uv-∫vdu

Let's choose u = x and dv = sinxdx. Then du = dx  v = -cosx

Let's substitute u, v and dv in the formula:

∫xsinxdx = (x)(-cosx)- ∫(-cosxdx)dx
              = -xcosx + ∫cosxdx
              =  -xcosx + sinxdx + C

Note. Using the integration by parts can be tricky in choosing u and dv. To avoid bumping into a new integral that's not easy to calculate, choose u to have a derivative easier to calculate. Choose dv into an integral easy to calculate. In general you can use the following guide:
1) Choose u to be the part whose derivative is simpler than u. Use dv as the remaining term.
2) Choose dv to be the portion whose integral can be calculated using the basic formula. Choose u as the remaining term.

Application:  In example 1, choose u and dv differently to see if the integral is easy to calculate.

Example 2. Evaluate ∫xe^xdx ( read x exponential x dx). The sign ^ is used to signify that x is the exponent of e.

We can choose u first and choose dv as the remaining term. If so the derivative of u should be simpler than u. We can choose dv first so that the derivative can be calculated using a basic formula and choose u as the remaining portion of the integral.

Let's choose u = x and dv = e^x dx. Then du = dx and v = e^x.
Applying the formula:  ∫xe^xdx = xe^x-∫ e^x.dx
                                                   = xe^x- e^x + C
Interested in learning more about integrals visit Center for Integral Development

An approach to calculate the area under curve: the definite integral

Let's suppose we have a function f and we want to calculate the area under its curve. It's not an easy thing to do. First, it is difficult to find the exact area under the curve. The easiest method would be to divide the area under the curve into a certain number of rectangles and to add these rectangles in order to get an approximation. The approximation is better if we divide the area in smaller and smaller rectangles.

Let's have a function f positive in an interval [x₀, x₄] and find the area under the curve of f between x₀ and x₄. The method consists of approximating the value of an area by dividing the area under the curve of (f) by a certain number of rectangles. Let's choose to divide the area under the curve into 4 rectangles of equal width Δx (delta x)


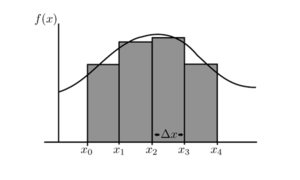
Let's name the area S(4). Then:

Let's divide S by 5 rectangles we have:

S(5) is greater than S(4) and represents better the area of the rectangle.
 .
The following simulation represents numerical values of the area S for a corresponding number of rectangles.

Each time we divide the area by a greater number the corresponding area approximates a greater number which is a better approximation. This fact is illustrated in the following figure:


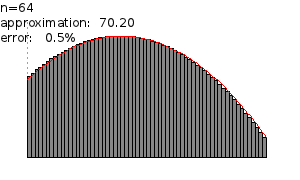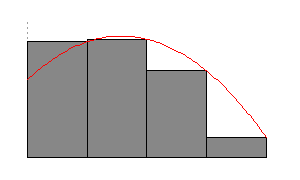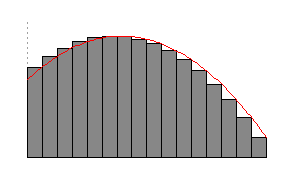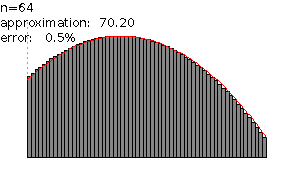
In the figure above for n = 1 the approximated area is 14.62. For n = 2 the approximation is 51.20. For n = 4 the approximation is 63.02. For n = 8, the approximation 67.32. For n = 16 the approximation is 69.07. For n = 32 the approximation is 69.84. For n = 64 the approximation is 70.20.

If we divide the area by n rectangles the area S(n) can be calculated by:

S(n) can be written as S(n) = Σ f(xi)𝚫x with i varying from 1 to n or:

As n comes to an extremely greater number the area approximates a greater number. The approximation becomes better and better and comes close to a greater number. This greatest number is the best approximation for the area of the rectangle. It is the limit of all the approximations when the number of rectangles n becomes extremely high. This limit is the limit of the function S(n). We write:

This value represents the integral of the function f between x0 and x1

We write:

Interested in learning more about Calculus visit Center for Integral Development

Rules of integration for combination of functions

If f and g are two integrable functions and C a constant, then we can derive the rules for the integration of the sum, difference of two functions as well as the multiplication of a function by a constant.

Integral of the sum of two functions

∫[f(x)+g(x)]dx = ∫f(x)dx + ∫g(x)dx

The integral of the sum of two functions is equal to the sum of the integrals of these functions. This rule is valid for the integral of the indefinite sum of functions. The integral of the sum of three functions is equal to the sum of the integrals of these three functions. The integral of the sum of four functions is equal to the sum of the integrals of these four functions. The integral of the sum of n functions is equal to the sum of the integrals of these n functions.

Integral of the difference of two functions

∫[f(x) - g(x)]dx = ∫f(x)dx - ∫g(x)dx

Integral of the product of a constant C by a function

∫(Cf(x)dx) = C∫(x)dx.