As in rectangular coordinates, if a solid S is bounded by the surfaces z = f(r, θ) and the surfaces r = a, r = b, θ = ɑ, θ = β, then the volume V of S can be found by integration using the formula:
If the base of the solid can be described as D = {(r, θ), ɑ ≤ θ ≤ β h₁(θ) ≤ θ ≤ h₂(θ)}, the volume V becomes:
Example
Solution
By the method of double integration, the volume is the iterated integral of the form:
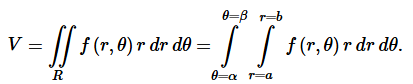



No comments:
Post a Comment