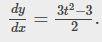Objective: to find the derivative of parametric curves
Derivatives of parametric equations
Let's consider the plane curve defined by the parametric equations:
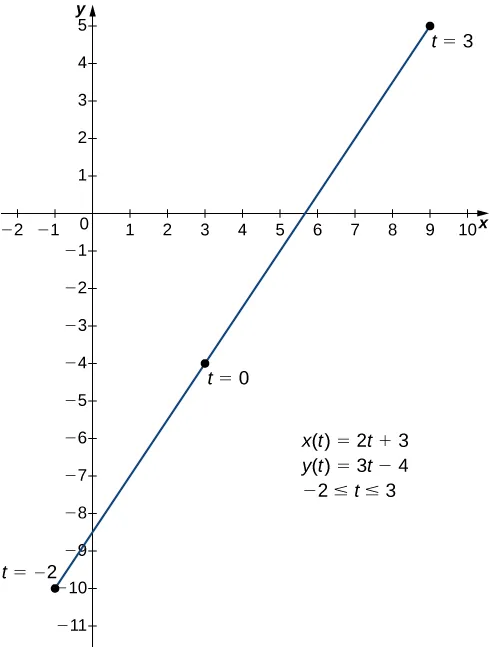
x(t) = 2t + 3 y(t) = 3t - 4 -2≤ x≤3
Our objective is to determine the derivative of the parametric equations. Let's note that the derivative of a function is a function that represents the slopes of all the tangent lines at different points of the curve. If we know the slope of a tangent line at a point we can know the slopes of all the tangent lines at different points of the curve of the function. The slope of a tangent line at a point is the derivative of the function at a point. The function that allows to find the derivative at a point allows to determine the derivatives of all points of the function. Determining the slope of a tangent line to the parametric curve will allow us to determine the derivative of the parametric equations.
The curve of the parametric equations is a line starting at (-1, -10) and ending at (9, 5).
Let's find the explicit form of the parametric equations. To do this we start by eliminating t in x(t):
Let's substitute t in y(t):
The slope of the tangent line is 3/2. The derivative is dy/dx = 3/2
But dy/dx = dy/dt/dx/dt = y'(t)/x'(t)
x'(t) = 2 y'(t) = 3
dy/dx = 3/2
In both cases dy/dt = 3/2. The expression dy/dx = y'(t)/x'(t) is the derivative of the function.
Theorem. Derivative of Parametric equations
Consider the plane curve defined by x = x(t) and y = y(t). Suppose that x'(t) and y'(t) exist, and then assume x'(t) ≠ 0. Then the derivative dy/dx is given by:
Examples
Calculate the derivative dy/dx for each of the parametrically defined curves and locate any critical points on their respective graph.
Solutions
a) Let's calculate dy/dx: dy/dx = y'(t)/x'(t)
From the parametric equations in example a) we have: y'(t) = 2 and x'(t) = 2. Therefore:
dy/dx = 2/2t = 1/t
A critical point is a point where the derivative is equal to zero or undefined. The derivative is undefined for t = 0. Let's determine the critical point. Substituting t in the parametric equations, we find x = -3 and y = -1. (-3, -1) represents the critical point. The graph of the curve is a parabola opening on the right and the point (-3, -1) is a vertex of this parabola.
b) I provided a guided solution for examples b) and c) .We have for example b)
Since the denominator is different of zero, the only critical points are those for which the numerator is equal to zero. That happens when t = -1 or t = 1 for which the critical points are: (-1, 6) and (3, 2) respectively. Here is the graph of the parametric curve.
The point (-1, 6) is a relative maximum and the point (3, 2) is a relative minimum.
c) We have : dy/dx = -cost/sint
The derivative is 0 for cost = 0. That happens when t = π/2 or t = 3𝛑/2 to which correspond respectively the critical points (0,5) and (0, -5).
When sint = 0, the corresponding values of t are : t = 0, t = π, t = 2π. The critical points are respectively:
(5. 0), (-5, 0) and (5. 0).
Here is the graph of the parametric equations defined in part example c)
Practice
Calculate the derivative dy/dx for the plane curve defined by the following equations and locate any critical points on its graph: