Representing a function as a power series

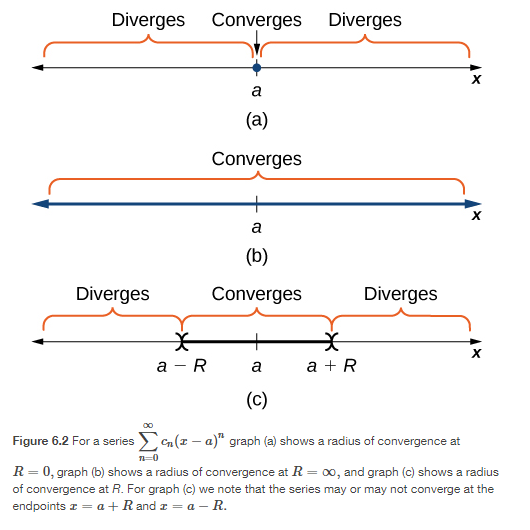
 If a power series converges to an expression representing a function, we can use the power series to represent the function. The function is then represented by an infinite polynomial. The polynomial expression can be used to differentiate or integrate the function. A truncated version of the polynomial expression can be used to approximate the values of the function. Let see how that can happen.

Let's consider the geometric series:

Let's recall that the following geometric series

converges if and only if ❘r❘<1. Therefore the series converges to a/1-a. 

Similarly the power series in x above converges if ❘x❘<1. It converges to 1/1-r. We can write:

In the following example we will show the power series provides a representation of the function f(x) = 1/1-x by comparing the graph of f with the graph of several of the partial sums of the power series.

Example 1

Solution

Let's graph f(x), S₂, S₄(x), S₆(x) in the interval (-1,1):

The graph shows a function and three approximations of it by partial sums of a power series. As N increases we get a better approximation of the function f

Example 2.

Solution

a) Let's recall that when ❘r❘<1 the series 

converges to a/1-r. Therefore a/1-r is the sum of the geometric series.

a/1-r = a + ar + ar² + .... (1)

Let's find a and r by writing the function f under the form a/1-r:

1/1+x³ = 1/1-(-x³)

We have a = 1, r = -x³. By substituting in (1), we get:

1/1+x³ = 1 + 1(-x³) + 1(-x³)² + ....= 1- x³ + x⁶ - ...

Since the series converges when ❘-x³❘<1, the interval of convergence is (-1,1)

Practice

Do example b)

  

 

  

The fundamentals of power series

 Learning objectives:

1. Identify a power series and provide examples of them

2. Determine the radius of convergence and the interval of convergence of a series

Definition  

A power series is a series with power of a variable. If the variable is x, the series holds power of x. Consequently a power series is an infinite polynomial. It is used to represent functions. A power series has the form:

where x is a variable and the coefficients cₙ are constants.

Example: The power series

is an example of a power series since it holds the powers of the variable x. It is a geometric series with ratio x. We know that it converges if ❘x❘<1 and diverges if ❘x❘>1.

Power series centered at x =a

A power series in the form

is a power series centered at x = a.

If a = 0, the power series is centered at 0. It's written as follow:

We stipulate that x⁰ = 1 and (x-a)⁰ = 1 even when x = 0 and x = a.

Examples:

1. The following series is centered at x = 2

2. 

are centered at x = 0.

Convergence of a power series 

One of the following is true:

1. The series converges at its center

2. It converges for all real numbers x

3. It converges in an interval

Theorem

Interval and radius of convergence. Definition

Graph of convergence of a power series

We apply the ratio test to determine the ratio test for a power series.

Examples

Solution

Note. It's better to do a discussion before concluding for the value of ρ according to the values of x. This value depends on a limit and an absolute value.

If x = 0, ρ = 0.1/∞ +1 =0

If x ≠ 0 ρ = ❘x❘.1/∞+1 = ❘x❘.0 =0. Therefore  ρ = 0<1 for all values of x  The series converges for all values of x

b. Let's apply the convergence test by calculating ρ :

Let's do a discussion here.

If x = 0, ρ = 0 ✕∞ (indetermination)

    If  x ≠ 0,  ρ = ∞. Therefore the series diverges for all values of x different of 0. Since it is centered at x = 0, it must converge at x = 0. Therefore the series convergences at the single point x = 0 and its radius of convergence is 0.

Practice

Find the interval and radius of convergence of