The fundamentals of power series

 Learning objectives:

1. Identify a power series and provide examples of them

2. Determine the radius of convergence and the interval of convergence of a series

Definition  

A power series is a series with power of a variable. If the variable is x, the series holds power of x. Consequently a power series is an infinite polynomial. It is used to represent functions. A power series has the form:

where x is a variable and the coefficients cₙ are constants.

Example: The power series

is an example of a power series since it holds the powers of the variable x. It is a geometric series with ratio x. We know that it converges if ❘x❘<1 and diverges if ❘x❘>1.

Power series centered at x =a

A power series in the form

is a power series centered at x = a.

If a = 0, the power series is centered at 0. It's written as follow:

We stipulate that x⁰ = 1 and (x-a)⁰ = 1 even when x = 0 and x = a.

Examples:

1. The following series is centered at x = 2

2. 

are centered at x = 0.

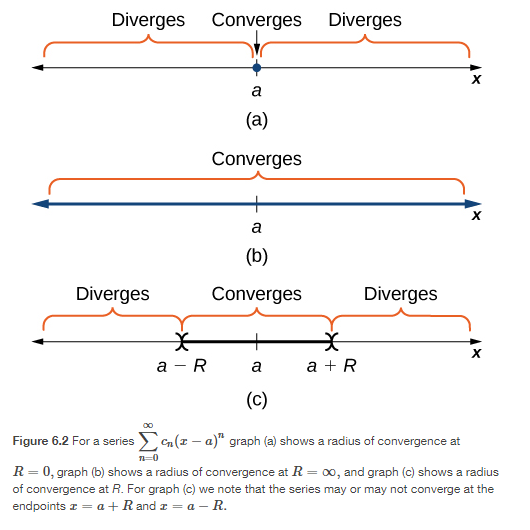
Convergence of a power series 

One of the following is true:

1. The series converges at its center

2. It converges for all real numbers x

3. It converges in an interval

Theorem

Interval and radius of convergence. Definition

Graph of convergence of a power series

We apply the ratio test to determine the ratio test for a power series.

Examples

Solution

Note. It's better to do a discussion before concluding for the value of ρ according to the values of x. This value depends on a limit and an absolute value.

If x = 0, ρ = 0.1/∞ +1 =0

If x ≠ 0 ρ = ❘x❘.1/∞+1 = ❘x❘.0 =0. Therefore  ρ = 0<1 for all values of x  The series converges for all values of x

b. Let's apply the convergence test by calculating ρ :

Let's do a discussion here.

If x = 0, ρ = 0 ✕∞ (indetermination)

    If  x ≠ 0,  ρ = ∞. Therefore the series diverges for all values of x different of 0. Since it is centered at x = 0, it must converge at x = 0. Therefore the series convergences at the single point x = 0 and its radius of convergence is 0.

Practice

Find the interval and radius of convergence of