The art of mastering the integration by parts

The integration parts allows to calculate the integral of the product of some functions. Let's derive a formula for it:

The formula for the derivative of a product is (uv)' = u'v + uv'

Then uv' = (uv)'-u'v

Let's integrate the 2 sides;

∫uv'dx = ∫(uv)'dx-∫u'vdx

∫u.(dv/dx).dx = uv-∫(du/dx).vdx

Let's simplify:

∫udv = uv-∫vdu

Example 1. Evaluate ∫xsinxdx;

Let's apply the formula: ∫udv = uv-∫vdu

Let's choose u = x and dv = sinxdx. Then du = dx  v = -cosx

Let's substitute u, v and dv in the formula:

∫xsinxdx = (x)(-cosx)- ∫(-cosxdx)dx
              = -xcosx + ∫cosxdx
              =  -xcosx + sinxdx + C

Note. Using the integration by parts can be tricky in choosing u and dv. To avoid bumping into a new integral that's not easy to calculate, choose u to have a derivative easier to calculate. Choose dv into an integral easy to calculate. In general you can use the following guide:
1) Choose u to be the part whose derivative is simpler than u. Use dv as the remaining term.
2) Choose dv to be the portion whose integral can be calculated using the basic formula. Choose u as the remaining term.

Application:  In example 1, choose u and dv differently to see if the integral is easy to calculate.

Example 2. Evaluate ∫xe^xdx ( read x exponential x dx). The sign ^ is used to signify that x is the exponent of e.

We can choose u first and choose dv as the remaining term. If so the derivative of u should be simpler than u. We can choose dv first so that the derivative can be calculated using a basic formula and choose u as the remaining portion of the integral.

Let's choose u = x and dv = e^x dx. Then du = dx and v = e^x.
Applying the formula:  ∫xe^xdx = xe^x-∫ e^x.dx
                                                   = xe^x- e^x + C
Interested in learning more about integrals visit Center for Integral Development

An approach to calculate the area under curve: the definite integral

Let's suppose we have a function f and we want to calculate the area under its curve. It's not an easy thing to do. First, it is difficult to find the exact area under the curve. The easiest method would be to divide the area under the curve into a certain number of rectangles and to add these rectangles in order to get an approximation. The approximation is better if we divide the area in smaller and smaller rectangles.

Let's have a function f positive in an interval [x₀, x₄] and find the area under the curve of f between x₀ and x₄. The method consists of approximating the value of an area by dividing the area under the curve of (f) by a certain number of rectangles. Let's choose to divide the area under the curve into 4 rectangles of equal width Δx (delta x)


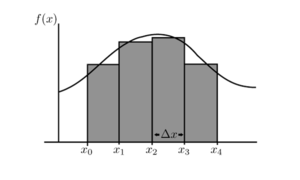
Let's name the area S(4). Then:

Let's divide S by 5 rectangles we have:

S(5) is greater than S(4) and represents better the area of the rectangle.
 .
The following simulation represents numerical values of the area S for a corresponding number of rectangles.

Each time we divide the area by a greater number the corresponding area approximates a greater number which is a better approximation. This fact is illustrated in the following figure:


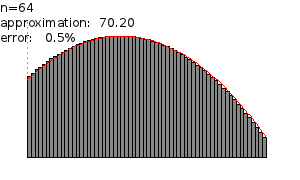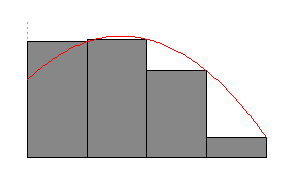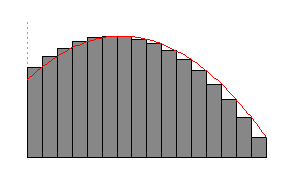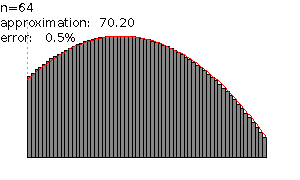
In the figure above for n = 1 the approximated area is 14.62. For n = 2 the approximation is 51.20. For n = 4 the approximation is 63.02. For n = 8, the approximation 67.32. For n = 16 the approximation is 69.07. For n = 32 the approximation is 69.84. For n = 64 the approximation is 70.20.

If we divide the area by n rectangles the area S(n) can be calculated by:

S(n) can be written as S(n) = Σ f(xi)𝚫x with i varying from 1 to n or:

As n comes to an extremely greater number the area approximates a greater number. The approximation becomes better and better and comes close to a greater number. This greatest number is the best approximation for the area of the rectangle. It is the limit of all the approximations when the number of rectangles n becomes extremely high. This limit is the limit of the function S(n). We write:

This value represents the integral of the function f between x0 and x1

We write:

Interested in learning more about Calculus visit Center for Integral Development