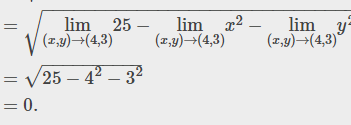Limit of a function of two variables at a boundary point

 Objective: Determine the limit of a function at a boundary point

Before to define the limit of a function of two variables at a boundary point, let's define interior and boundary point.

Interior point.

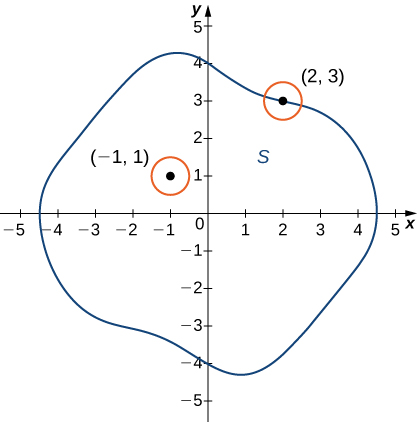
Let's consider a subset S of R². A point P is an interior point of S if any δ disk centered at P is located completely inside of S. Example: the point (-1, 1) in the figure below is an interior point

Boundary point

A point P is a boundary point if any δ disk centered at P is not completely located inside of S. It means that  some points of the disk are located inside of S and others are located outside of S. Example: the point (2,3) is a boundary point.

Definition of the limit of a function f at a boundary point

Let f be a function of two variables x and y and (a, b) be on the the boundary of the domain of f. Then the limit of f(x,y) when (x,y) approaches (a,b) is L written:

if for any ϵ > 0. there exists δ>0 such that for any point (x,y) located inside the domain of and within a suitable small distance δ of (a,b), the value of f(x,y) is no more than ϵ away from L. Using symbols we write: for any number δ >0, there exists ϵ>0 such that

Example

Solution

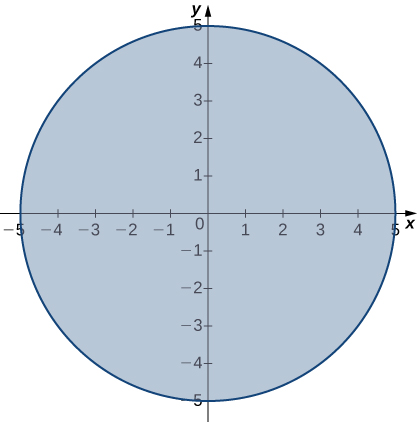
The domain of the function:

 

 is a circle of radius 5 centered at the origin along its interior as shown in the figure below

Let's calculate the limit of the function by applying the limit rules which apply to the boundary of the domain of the function as well the interior points of the domain.

Here is the graph of the function                                                                                                              :

                                                                                                                       
Practice                                                                                                                                                

Evaluate the following limit: