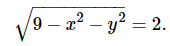Level Curves

 Civil engineers building roads in mountains use a topographical map that shows the different elevations of the mountain. Hikers walking through rugged trails use also a topographic map to show how steeply the trail changes.  A topographical map contains curved lines called contour lines. Each contour line corresponds to the points of the map that have the same elevation. A level curve of a function of two variables f(x,y) is similar to a contour line in a topographic map.

The photo on the left is a topographical map of the Devil's Tower, Wyoming. USA. Lines that are close together indicate very steep terrain. The picture on the right was taken in perspective. It shows how steep the sides of the tower are. Notice that the top of the tower has the same shape as the center of the topographical map. 

Definition.

Given a function f(x,y) and a number c of its range, a level curve of the function with two variables f(x, y) for the value c is the set of points that satisfy the equation f(x, y) = c. A graph of the various level curves of a function with two variables is called a contour map.

Example 

Let's consider a previous function:

Let's determine the level curves of this function, The range  of this function is the closed interval [0.3]. let's choose any number in this interval, for example c = 2. The corresponding level curve is given by the following equation:

Let's square both sides of the equation. We have:

Let's multiply both sides by -1 and add 9 to both sides:

This represents the equation of a circle of radius ⎷5 and centered at the origin. This is one level curve of the function. Choosing different values of c lead to other level curves. For c =3 and substituting this value in the function, we obtain x₂² + y² = 0, which is the origin. For c = 0, we have  x₂² + y² =9, which is the circle centered at the origin and radius 3, For c = 1, we have  x² + y² = 8, which is the circle centered at the origin and of radius 2⎷2. The contour map of the function is shown below:

 

Graph of functions with two variables (continued)

 In this post, we continue with examples. We are going to solve a practical problem concerning nuts and bolts.

Problem

A profit function for a hardware manufacturer is given by:

where x is the number of nuts sold per month (measured in thousands) and y the number of bolts sold per month (measured in thousands). Profit is measured in thousands of dollars. Sketch a graph of this function

Solution

Let's determine the domain of the function. This function is a polynomial function with two variables. For a profit to occur, we need to have f(x,y) ≥ 0. In other terms:

 

 

This is a disk of radius 4 centered at the point (3, 2) where x and y must be non-negative. When x = 3 and y = 2 f(x, y) = 16. Note that x and y can be non-integers. For example it is possible to sell 2.5 thousands nuts per month. The domain contains thousands of points. We can consider all points within the disk. For any z<16, we can solve the equation f(x,y) = z.

The second side of the last previous equation represents the square of the radius of the circle  with center (3,2). Therefore this expression must be strictly superior to zero.: 16-z>0. Therefore z<16. 

The range of f(x,y) is:

The graph of f(x,y) is a paraboloid pointed downward.

Graph of a function of two variables

 Goal: graph of a function of two variables

Graphing of a function of two variables

A function z = f(x,y) is a function with two independent variables x and y and one independent variable z. The graph of a function of one variable y = f(x) is made of of all the ordered pairs (x,y) in the cartesian plane. The pair is made of two elements  where the first element is an independent variable and the second element is a dependent variable. Similarly the graph of a function with two variables is made of triples (x,y,z) where x and y are independent variables and z is the dependent variable. The graph of a function z = f(x,y) is called a surface.

To understand the concept of graphing a function z = f(x,y) to obtain a surface in three dimensional space, let's imagine the coordinate system (x,y) laying flat. Every pair (x,y) in the domain of the function has a unique point z associated with it. If z is positive, then z is located above the xy plane. If z is negative, then z is located below the xy plane. The set of all the graphed points becomes the three dimensional surface that is the graph of the function.

Example :

 

Solution

In the example of the previous post, we determined that the domain and range of: g(x,y) = ⎷9-x²-y² are respectively:

and

When x² + y² = 9, g(x,y) = 0. Therefore, any point on the circle of radius 3 is mapped to the point z = 0 in R³. When x² + y² = 8. g(x,y) = 1. Therefore, any point on the circle centered at the origin and of radius 2⎷2 is mapped to z =1 in R³. As x² + y² gets closer to 0, z gets closer to 3. When x² + y² = 0, g(x,y) = 3. This is the origin in the xy plane. If x² + y² is equal to any other value between 0 and 9, g(x,y) takes any value between 0 and 3. The surface described by this function is an hemisphere of radius 3 as shown in the figure below.                                                                                             

This function contains also  x² + y². Setting this expression equal to various values starting at 0, we obtain circles of increasing radius. The minimum value of f(x,y) = x² + y² is 0 (obtained when x = 0 and y = 0). When x = 0, the function becomes z = y². When y = 0, the function becomes z = x². These are cross-sections of the graph and are parabolas. The graph of f is shown below:

Functions of two variables

 Goal: recognize a function of two variables and identify its domain and range

Function of two variables

The definition of a function with two variables is similar to that of the function with one variable. The only difference is that we map a pair of two variables to another variable instead of mapping one variable to another variable.

Definition

A function of two variables z = f(x,y) maps each ordered pair (x,y) in a subset D of the real plane R² to a unique real number z. The set D is called the domain of the function. The range of f is the set of all real numbers z that has at least one ordered pair (x,y) 𝜺 D such that f(x,y) = z as shown in the following figure:

Examples                                                                                                                                                      

                                                                                                                                                  

Solution

a. This is an example of a linear function with two variables. There is no pair of variables (x, y) for which the function is not defined. Therefore the domain of the function is R².

To determine the range of the function, let's determine the set of reals z for which f(x,y) = z. We have 3x +5y + 2 = z. Let's solve this equation by choosing x = 0. We have 5y + 2 = z. y = z-2/5. The pair (0, z-2/5) is a solution of the equation 3x + 5y + 2 = z for any value of z. The range of the function is R.

b. For the function g to have a real value we need 9 - x² - y²≥ 0 or  - x² - y²≥ -9  x² + y² ≤ 9  

The domain D is defined as follow: D = {(x,y)ε R²/ x² + y² ≤ 9}.The graph of this set of points is described as a disk of radius 3. The graph includes the boundary as shown below.

    To determine the range of the function, we have to find out the set of reals for which g(x,y) = z.  The domain is made of circles starting from (0, 0) and ending at the boundary circle defined by x² + y² = 9. Let's find z for (0,0) i.e a point of the domain starting at the origin. We have g(0,0) = z. 

g(0,0) = ⎷9-(0)²-(0)² = ⎷9 = 3. Let's take a point of the boundary circle i.e (0,3). We have g(0,3) = ⎷9-(0)² - (3)⁰ = 0. The range is [0,3].

Practice

 

Arc length in polar curves (continued)

 In the last post, we set the formula for the arc length of a polar curve. Now let's do an example. 

Example

Solution

  When θ = 0, r = 2 + 2cos0 = 2 + 2 = 4.  As θ goes from 0 to 2ℼ, the cardioid is traced exactly once. Therefore 0 and  2ℼ represent the limits of integration. Using f(θ) = 2 + 2cos0 , ɑ = 0 and β = 2π , the formula for the arc length becomes:                                                                                                         

                                                                                                       

We have 1 + cosθ = 2cos²θ/2. Multiplying by 2: 2 + 2cosθ = 4cos²θ/2.                                         

                                                                                                                     

                                      

The absolute value is necessary because cosine is negative for some values of its domain. To resolve this issue, change the limit from 0 to ℼ and double the result. This strategy works because cosine is positive between 0 and ℼ/2 .                                                                                                               

 

Practice  

Find the arc length of r = 3sinθ                                                                                                                                           

                                                              :