We continue with solving problems of volume of solids in polar coordinates using double integrals. Here is another example.
Example 2
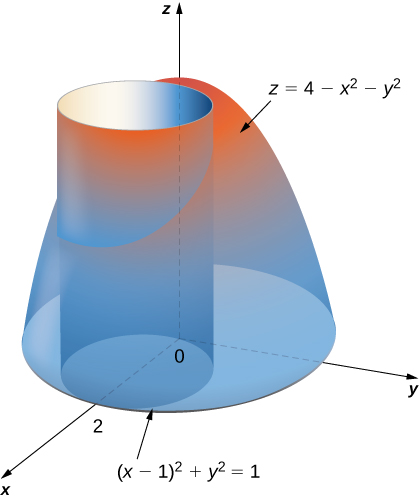
Solution
Let's first express the equation of the region which is a disk in polar coordinates. We need to find θ and r.
The equation of the disk can be expressed as::
This is a set of circles with radiuses less than or equal to1. These circles are centered in (1,0). The center can be found by rewriting the left part of the above inequality as (x-1)² + (y-0)². The angle θ varies from 0 to 2ℼ..Expanding the square term in the equation (x-1)² + y² = 1, we have:
By simplification, we get :
By substituting x = cosθ and y = sinθ, we have:
Solving this equation, we find:
The disk on the xy plane can be expressed on the following region as:
Let's calculate the volume. We have:
Let's calculate the inner integral:




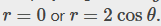





No comments:
Post a Comment