Volume of a solid of revolution: method of disks

In the previous post we define the formula to find the volume of a solid which consists in integrating the area of a cross-section. In the following post I am going to find another version of this formula using the method of disks.

 Method of disks

Let f be a function continuous and positive in an interval [a,b]. Let’s consider a region R between f and the x-axis. Let’s R revolve about the x-axis. This action generates a solid of revolution with cross-circular sections with radii f(x) for any value of x.

Volume formula by the method of disks

In the previous lesson we learn that the volume of a solid is found by integrating the area of the cross-circular section within a definite interval.

Example

Calculate the volume of the solid that is obtained when the region under the curve x  is revolved about the x−axis over the interval [1,7].

Solution

Here is the graph of the function f:

We revolve the region between f(x) and the x-axis. We obtain the following figure:

Since the cross-section is circular, the volume of the solid is given by:

Practice
.
Demonstrate that the volume of a sphere with radius r is V = 4𝛑r³/3

Interested in Calculus tutoring visit New Direction Education Services
Interested in learning Calculus online visit Center for Integral Development

Application of integral: the volume formula

In arithmetic we learn the formula to calculate the volume of a  a solid such as a cube. The problem is we have to memorize the formulas for every figure. The definite integral allows us to find a general formula  for the volume of any solid.
Let's consider a cubic solid limited by two parallel planes perpendicular to the x-axis. At any point x, any plan perpendicular to the x-axis is called a cross section.


In order to find the volume of this solid, we are going to divide it in different slices of widths 𝝙x₁, 𝝙x₂, 𝝙x₃ 𝝙xn. This leads to divide the interval [a,b] into different sub-intervals of lengths 𝝙x₁, 𝝙x₂, 𝝙x₃ 𝝙xn. Let's A₁, A₂, A₃... An be the different cross-sections or base of the cubic slices. The volume of the cube is equal to the sum of the volume of the different slices.

V = A₁𝝙x₁ + A₂𝝙x₂ + A₃𝝙x₃ + An.𝝙xn.

There is a way to write this sum simpler:

Let's divide each slice into more slices. We now have thinner slices. Let's continue to divide each slice into more slices. The slices become thinner and thinner. At each time we get a better approximation. We can notice also that each time we divide each slice the width becomes smaller and smaller. It means that 𝝙x approaches zero. When this is the case v approaches a certain value. This value represents the limit of the sum and is the value of V. We can write;

This value represents the definite integral of the function A(x) when Δx approaches zero. We can finally write in the integral form:

Application

Let's demonstrate that the volume of a pyramid is equal to one third the area of its base by its height.
If a is the length of the sides of the base and h the height V = 1/3 a²h



Since the cross section is perpendicular to the y-axis we have to integrate in respect to y. Then the volume of the pyramid can be calculated by

The cross-section A(y) varies from o to h therefore the volume V becomes

A(y) is a square of sides b. Therefore its area is b². We have A(y) = b².

Let's calculate b. To do that, let's isolate from the figure above the triangle with height h

Interested in Calculus tutoring visit New Direction Education Services

Interested in learning Calculus online visit Center for Integral Development

Area between two curves

Objective: Find the area between two curves

Method

Let's consider 2 functions f and g. We want to find the area limited by the curves of these functions and the verticals x = a and x = b.

.
The area limited by the the curves of f and g  and the two verticals passing respectively by x = a and x = b can be found by subtracting the area under the curve of g from the area under the curve of g.

Let A be the area between the 2 curves we can write:
A = Area under f-Area under g
The area under f and limited by the verticals passing by a and b and the x-axis is given by

The area under g limited by the verticals passing by a and b and the x-axis is given by

Let's substitute area under f area under g in A

According to this result, we can make the following statement:

Let f and g be two continuous functions on the interval [a,b] and f(x)≥ g(x) for all values of x in this interval, then the area between the the curves of and g is given by

Example

Solution

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                             
Practice 

Sketch the region enclosed by the curves of y = x²and y = x + 3. Find the area. 

Interested in math tutoring including Calculus visit New Direction Education Services  
Interested in learning Calculus online visit Center for Integral Development                        

Applications of integral: area between a curve and the x- axis

Objective: Find the area between the curve of a function f and the x-axis over an interval [a b].

Definition

The area between the curve of a function and the x-axis bounded by the verticals x = a and x = b is given by

The area is positive if it is located above the x-axis and negative if it is below.



The areas A(2), A(4) are negative. The areas A(1), A(3) and A(5) are positive. The total area is the sum of all the areas: positive and negative.

Example 



Solution

Practice

  

 

         Interested in math tutoring including Calculus visit New Direction Education Services. Interested in learning Calculus online visit Center for Integral Development                                                                                                                                               

Fundamental theorem of Calculus

Fundamental theorem of Calculus

This theorem is divided in two parts:

1. First fundamental theorem of Calculus

The derivative of the integral of a function f with respect to the variable t over the interval [a, x] is
equal to the function f with respect to x. This is expressed by:


This theorem shows the relationship between the integral and the derivative. It tells us that the integral of a function f can be calculated by taking its integral over a variable bound of integration.meaning that the upper limit of integration is variable. In fact the above relationship shows that when we take the derivative of the integral we find the initial function f.

2. Second fundamental theorem of Calculus

The definite integral of a function f over an interval [a,b] is equal to the antiderivative at b minus
the antiderivative at a. If a function f is continuous over an interval [a,b] and F is an antiderivative
of f over this interval, then:


This theorem shows the relationship between the definite integral and the indefinite integral.

Practice

1. Evaluate:

Solution



2. Use the fundamental theorem of Calculus to find the derivative of



N.B. In this exercise it's dt instead of dx.

Solution



Exercise

Find the derivative of:


Interested in learning more about Calculus visit Center for Integral Development

Methods of resolution of the improper integrals

Objective: Solve the different types of improper integrals

Definition. An improper integral is an integral  where one or  the two limits of integration are infinite. An integral is also improper when the function has an infinite discontinuity. Let's look at the two scenarios:

I. One or two of the limits of integration are infinite.

a. One of the limit of integration is finite,

If f is continuous over the interval [a, +∞[, then

If the limit is finite the integral converges. If the limit is infinite the integral diverges.                                                                                                                                                          

Geometric Interpretation

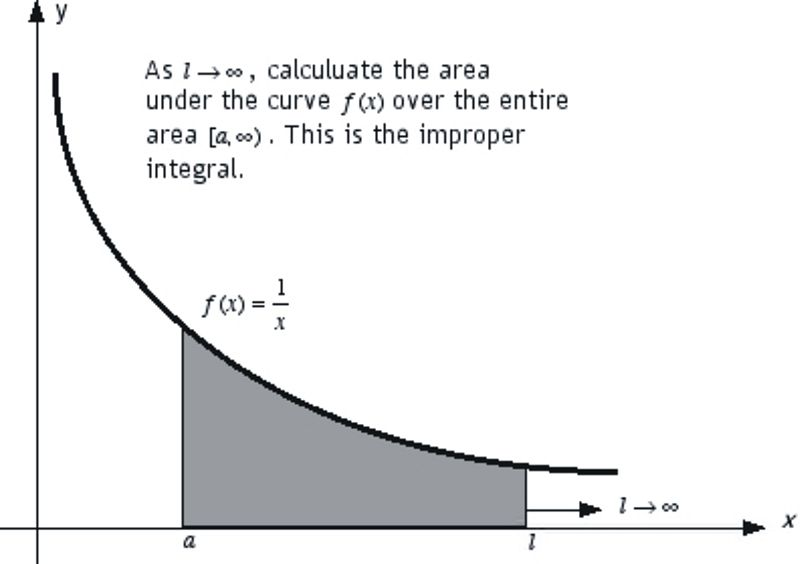
Let's consider a function f(x) = 1/x. The integral  represents the area under the curve of the function that starts from the vertical passing by a and extending to infinity.
The integral  represents the area between the verticals passing by a and l. As l approaches infinity, the area under the curve spreads to infinity. It's fair to say that this situation represents  .
 We can define  as the limit of   when l approaches infinity.
We can then set a rule to calculate the improper integral where the lower limit is finite and the upper limit is infinite. In this case we have to replace the infinite limit by l and find the limit of   when l approaches infinity.

Example 1. Calculate 

Solution

Let's replace infinity by l and calculate the limit of the finite integral when l approaches infinity.

We have:

    b. The two limits of integration are  infinite                                                                                

  In this case we choose any value a in the interval ]-∞, +∞[ and calculate the integral over the sub-intervals

 ]-∞, a[∪ ]a ,  +∞[                                                                                                                                  

Example 2. Evaluate                                                                                                     

                                                                                                                            

Solution

Let's split the integral over the intervasl ]-,0] and [0,+[:

                                                                                                                                         

                                                      

Let's evaluate the first integral on the right side:                                                                           

                                                                                                                                                         

Let's calculate the limit by substituting l by -∞:                                                                                          

                                                                                                                                                        

Let's evaluate the second integral:                                                                                                      

                                                                                                                                                      

     Let's substitute the two integrals we obtain:

II The function to integrate is discontinued.

Let's say that we have to calculate an integral over an interval ]a, b[ where the function f is continued. If the function isn't continued at a point c of the interval, we evaluate the integral over the intervals ]a,c[∪]c,d[.

Example. Evaluate 

Solution

The function is discontinued at x = 1. Therefore we integrate it over the 2 intervals ]0,1[∪ ]1.4[.


Let's calculate the first integral:

= ln │1⁻-1│-ln1
= ln o⁺
= -∞

  Since the first integral diverges there's no reason to calculate the second integral. The given integral diverges.

Exercises                                                                                                                                                           
Evaluate. Tell if the integral converges or diverges:

If you want to learn more about Calculus check this site Center for Integral Development
.