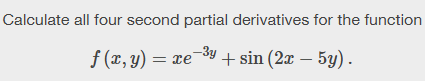Higher order partial derivatives of a function of two variables

 Objective: Find all second order partial derivatives of a function of two variables

High order partial derivatives

Let's consider a function of two variables. We can calculate the partial derivatives of this function. If we calculate the partial derivatives of the first partial derivatives, we obtain second order partial derivatives. If we calculate the partial derivatives of these second order partial derivatives, we obtain third order partial  derivatives and so on.

Let's consider the function:

Its partial derivatives are:

The partial derivatives of these partial derivatives are:

𝛿²f/δx² = 8x and δ²f/δy² = -8x + 30y. These new partial derivatives are called second order partial derivatives.

There are 4 second order partial derivatives of any function provided they all exist

Example

Solution

Practice

Partial derivatives of a function of three variables

 The partial derivative of a function of three variables can be calculated the same way we calculate the partial derivatives of a function of two variables. To calculate the partial derivative with respect to x, we consider y and z constants then we calculate the derivative considering only x as a variable. In general to calculate the partial derivative to one variable, we calculate the derivative with respect the considered variable while we keep the other two variables constant.

Definition

Example

Solution

To  calculate the partial derivative with respect to x using the limit definition, let's start by using the formula                                                                                                                                              

Let's start by calculating f(x + h, y, z):                                                                                                         

Let's substitute f(x+h, y, z) and f(x,y,z) in the formula:                                                                                   

                                                                                                     

Practice                                                                                                                                                     

Limit of a function of three or more variables

 Function of three or more variables

Let's consider two functions respectively of three and four variables that have applications in the real world. Let' f(x,y,z) be a function that measures the temperature at a location (x,y,z) and f(x,y,z,t) a function that measures the air pressure at a time t. How can we take the limit of a function in R³? What does it mean for a function of three or more variables to be continuous?

The answers to these questions start by extending the notion of a δ disk in a function of two variables to functions of three or more variables. The notions of limits and continuity for these functions are similar to those of a function of two variables.

Definition of a δ ball

The notion of δ intervenes in the definition of a function in any dimension. It is a neighborhood located in the domain of definition of a function. In a function of one variable, it is represented by a line. This line represents al the points x of which the distance from a central point is less than ẟ. In a function of two variables, it is represented by a disk. This disk represents all the points located within the distance of the radius of a circle centered a point (x₀, y₀) than In a function of two or more variables it is represented by a ball which represents all the points located with the distance of the radius of the ball. The ball is also called sphere. Here is the definition:

 

Limit of a function of three or more variables

The limit of a function implies two neighborhoods: one in the domain of the function and the other in the range. To show that the limit of a function at a point located in the domain of the function exists, we need to find a neighborhood located around that point such that for any point located in that neighborhood the value of the function at that point is close to a fixed value  called the limit of the function. This consideration is valuable for a function in any dimension.

In two dimensions the definition states as follows:

In three dimensions we have:

In 4 dimensions we have:

Example 

Solution

Practice

Find the limit of the following function:

 

Level surface of a function of three variables

Objective:  Find the level surface of a function of three variables.

In a function of two variables, we have level curves which are defined in the xy plane. In a function of three variables, level curves are called surfaces

Definition

Level surfaces in a function of three variables

There are several types of level surfaces depending on the form of the function of three variables. Let's limit ourselves to three types.: planes, quadric surfaces and spheres.  

Plane

When the function f(x,y,z) is a linear function leading to the equation  ax + by + cz = d where a,b, c and are contants, the level surface is a plane. Planes are flat, have no curvature and extend infinitely.

Quadric surfaces

If the function f(x,y,z) is a quadric function leading to the equation ax² + by² + cz² = d which is a second degree polynomial, the level surface is a quadric surface. Quadric surfaces can be ellipsoid, hyperboloid, paraboloid, cone and cylinder depending on the form of the quadric equation.

Ellipsoid

Hyperboloid

There are two types:

1.Hyperboloid of one sheet

 

2. Hyperboloid of 2 sheets

Consists of two separate surfaces like two bowls facing each other.

Equation:

Paraboloid

There are two types:

 

Cone

Sphere

Example

Solution

Practice

Find the level surface of the function of 3 variables and describe it:

a) 

 

b)