Applications of double integrals in Probability

One application of the double integrals over general regions is found in calculating the probability of two random variables. Let's start by defining some notions.

Density function of one variable

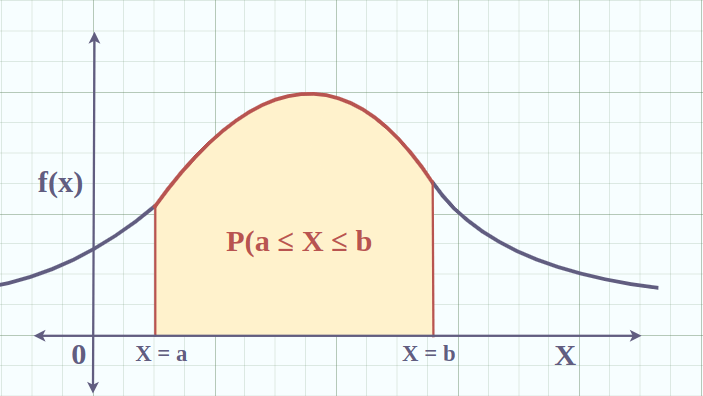
  Let's consider the following figure:

Let's consider the point (a, f(a)) of the curve. f(a) represents the probability density of this point. Likewise  f(b) represents the probability density corresponding to the point (b, f(b)). Any point of the curve  has a density probability. The area under curve between X = a and X = b represents the sum of all the probability densities of all the points of the curve between f(a) and f(b).. It represents the integral of the function f over the interval [a, b]. It represents also the probability that any variable between a and b falls between the range [a. b]. The function f is the probability density function of f over [a, b].

Joint Density function of two variables

The notion of probability density function of one variable can be extended to two variables. Since we deal with two variables, we use double integrals. The probability density of two variables X and Y is called joint probability density. In this case, the probability density function of two variables X and Y is called joint probability density function. 

Definition I

Let's consider a pair of continuous variables such as the birthdays of two people. The probability that the pair (X,Y) falls in a certain region D is given by:

Definition II

The variables X and Y are said to be independent random variables if their joint density function is equal to the product of their individual density function.

Example

Solution

 

 

 

Improper integrals on an unbounded region

 We previously evaluated a double integral on a bounded region. What if the region is unbounded? The following theorem comes handy for our rescue.

Theorem

Example

Solution

Practice

Improper Double Integrals

 Definition of an improper integral

It's preferable to deal with improper integrals of functions over rectangles or simple regions where these functions have finitely many discontinuities. However, not such improper integrals can be evaluated. A form of Fubini's theorem allows to evaluate some types of improper double integrals.

Fubini's theorem for improper integrals

Two conditions are necessary for the theorem to work. The function has to be nonnegative on D and has many finitely discontinuities inside D.

Example

Solution

Let's start by plotting the region. 

The function f is continuous on all points of the region D except in (0,0). If you keep the expression of the region, it would be difficult to calculate the double integral. However, if we express the region in 

the following way, the double integral becomes easy to calculate.

Practice

Consider the function f(x,y) = sin(y) /y over the region:

Finding the average value of a function with 2 variables

 We have seen previously that double integrals can be used to calculate volumes and areas. We can also use double integrals to find the average value of a function with 2 variables. 

Definition

If a function f(x,y) is integrable over a plane bounded region D with positive area A(D), then the average value of f is given by:

Note that the area is:

Example

Find the average value of the function f(x,y) = 7xy² on the region bounded by the line y = x and the curve x = ⎷y.

Solution

The figure above represents the region bounded by the line y = x and the curve x =⎷ y

First find the area A(D) where the region D is given by the figure above. We have:

Then the average value of this function over the given region is:

  Practice                                                                                                                                                         

                                                                                                                                                     

 

Calculating areas using double integrals

 Objectives:

1) Finding the area of a rectangular region

2) Finding the area of a nonrectangular region

We can use double integrals to find the area of a rectangular region and a nonrectangular region

Area of a rectangular region

The area of a single rectangular region can be found by a simple geometric formula. It can also be found using double integrals.

By definition, the area of a plane bounded region D is given by:

Area of a nonrectangular region

We have seen that an area can be calculated using a single integral. It can also be calculated using double integrals.

Example

Find the area of the region bounded below by the curve y = x² and above by the line y = 2x in the first quadrant.

Solution

Practice

Visit this Calculus site: Learn Calculus Easily

Join the Calculus Facebook group: