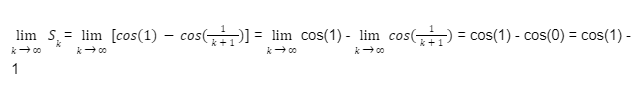What is a p-series?

 Learning objectives. 

1) Define what a p-series is?

2)  Determine if a p-series converges or diverges

Definition

For any real number p, the series 

is called a p-series. As examples the following harmonic series are p series:

Convergence and divergence 

A p-series converges if p>1 and diverges if p≤1

Examples

Determine if each of the following series converges or converges:

Solution

a) Here we have p>1 or 4>1. Therefore the series converges

b) p≤1 or 2/3≤1. The series diverges.

Practice

Determine if the following series:

converges or diverges.

The Integral test for convergence and divergence of series

 The objectives of this post are:

1) Know what the integral test is about

2) Use it to determine if a series is convergent or divergent.

Integral test

We have studied so far different types of series: geometric, harmonic, telescopic. The study of these series show easily if they are convergent or divergent. At the beginning we state that the determination of the convergence or divergence of a series leads to the determination of the convergence or the divergence of the sequence of partial sums. This leads to determine the general term of the partial sums. This is something really complicated. Some other alternative methods make it easier to study the convergence or divergence of a series. The divergence test is one of them. Now we are going to use the Integral test which assimilates the series to an improper integral.

Theorem 

Let's suppose that f is a positive, continuous and decreasing function on the interval [k, n) and f(n) = aₙ then

Example 1. Assuming that all the conditions for the integral test are met determine if the following series converges or diverges.

Solution

Let's compare :

Let's calculate the integral:

The integral is convergent. Therefore the series is convergent

Example 2 . Same question with the series

Solution

In the example above we use the constant b as the upper limit of the integral. We can use any letter as the upper limit. In this example use the letter t.

Let's compare:

Let's calculate the integral on the second side:

We do the substitution u = lnx . Therefore du = (1/x)dx. Then:

Let's substitute the integral in the line above by its calculated value:

The integral diverges so is the given series.

Practice

Determine if the following series is convergent or divergent

Telescoping series

 Learning objectives:

1) Define the telescoping series

2) Determine if a telescoping series is convergent or divergent

Definition

A telescoping series is a series in which most of the terms cancel out leaving only the first and the second term. In fact the following series is a telescoping one

Let's verify that by calculating some of the partial sums:

In each of these partial sums, we can see that they are the difference between the first and the last term.

From these partial sums, the general term of the partial sums can be written as: Sₖ = b₁ - bₖ₊₁.

Convergence

The series is convergent if the sequence of the partial sums is convergent. To find out about this, we have to look for the general term of this sequence and calculate its limit. Therefore we have to find the limit of 

Sₖ = b₁ - bₖ₊₁. when approaches infinity.

Example. 

Determine whether the telescoping series:

 

converges or diverges. If it's convergent, find its sum.

Solution

Let's find the general term of the sequence of the partial sums by calculating the first few ones:

 

According to the pattern found from these partial sums, the general term can be written as:

Let's find lim Sₖ when n approaches ∞

The series is convergent and converges to cos(0) - 1. Therefore:

Practice

Harmonic Series

 Definition

An harmonic series is a series in the form:  

 Divergence

A harmonic series is divergent. This can be demonstrated through the Integral test or other method

Example

 Show that the following series is divergent:

Solution

As written above the harmonic series can be written as:

Let's replace the sum of all the terms after the third term by:

Then we have:

Let's solve this equation for 

The series in the second side is divergent as an harmonic series. Being an harmonic series, its value can be infinite or it doesn't have any value at all. Substracting a finite value from infinity or an indefinite value doesn't change infinity or the indefinite value. The harmonic series in the second side remains divergent. Therefore the series in the first side is divergent,

Practice

 Show that the following series is divergent:

Geometric series

 Definition. A geometric series is a series in the form:

a is called the initial term because it is the first term, r is called the ratio.

Example: 

is a series with initial term 1 and ration r = 1/2

Convergence and Divergence

In the geometric series having the form above

If ❘r❘ <1, the series converges. The series can be written as:

It  converges to a/1-r

If ❘r❘≥1, the series diverges.

Exercises

Determine whether the following series converges or diverges. If it converges find its sum:

Solutions

a) Let's find the first several terms in the series:

 

 

The initial term is the first term. We can see that it's repeating in the following term as a product of itself by the power of another term. The initial term here is a = 9 and the ratio is -3/4. Since ❘-3/4❘<1, the series converges. It converges to a/1-r = 9/1-(-3/4) = 9/1+3/4 = 9 /7 over 4 = 36/7. The series converges to 36/7

b) 

Practice

Considerations on convergence and divergence of series

 In a previous post, to determine if a sequence is convergent or divergent we had to find the limit of the sequence of partial sums  . To do this, we had to determine the general term of the sequence of partial sums and find its limit. This is a tedious work to find the formula of the general term of the partial  sums. There are different other ways to determine if a series is convergent or divergent. One of them is called the Divergence Test. We will explore the other ways later. Before exploring the divergence test, let's see what happens when a series converges. 

Theorem. If Σaₙ converges then lim aₙ = 0 when n approaches infinity. 

This statement means that if a series converge, then lim aₙ will necessarily be equal to zero when n approaches infinity. The converse of this statement is not true. This means that if  lim aₙ = 0 when n approaches infinity, the series doesn't necessarily converge. There are series of which the limit is equal to zero but they are not necessarily convergent. 

 Divergence Test.

The divergence test allows to quickly conclude if a series is divergent. But if the limit is equal to zero, we don't know if the series is convergent or divergent. We say that the divergence test is inconclusive. The divergence test is stated like this: If lim a #0 when n approaches infinity then Σ aₙ diverges

Example. Determine if the following series is convergent or divergent.

Let's calculate lim aₙ when n approaches infinity.

The limit is different of zero, therefore the series diverges.

Practice