Learning objectives:
1) Define the telescoping series
2) Determine if a telescoping series is convergent or divergent
Definition
A telescoping series is a series in which most of the terms cancel out leaving only the first and the second term. In fact the following series is a telescoping one
Let's verify that by calculating some of the partial sums:
In each of these partial sums, we can see that they are the difference between the first and the last term.
From these partial sums, the general term of the partial sums can be written as: Sₖ = b₁ - bₖ₊₁.
Convergence
The series is convergent if the sequence of the partial sums is convergent. To find out about this, we have to look for the general term of this sequence and calculate its limit. Therefore we have to find the limit of
Sₖ = b₁ - bₖ₊₁. when approaches infinity.
Example.
Determine whether the telescoping series:
converges or diverges. If it's convergent, find its sum.
Solution
Let's find the general term of the sequence of the partial sums by calculating the first few ones:
According to the pattern found from these partial sums, the general term can be written as:
Let's find lim Sₖ when n approaches ∞
The series is convergent and converges to cos(0) - 1. Therefore:
Practice






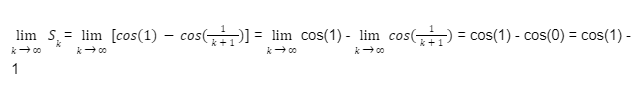


No comments:
Post a Comment