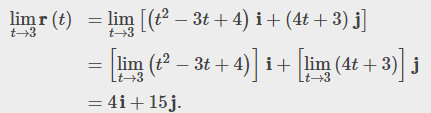Integrals of Vector-valued Functions

 Goal: Calculate the integral of vector-valued functions

Integrals of vector-valued functions

The antiderivative and definite integral of vector-valued functions can be calculated by taking the antiderivative and definite integral of the real-valued functions. This is the same way we have been doing with the derivative.

The antiderivative of a vector-valued function appears in applications. For example, if a vector-valued function represents the velocity of an object at a time t, then its antiderivative represents its position. Or, if the function represents the acceleration of the object at a given time, then the antiderivative represents its velocity.

Definition

Let f, g, h be real-valued functions integrable over the closed interval [a, b].

1. The indefinite integral of a vector-valued function r(t) = f(t)i + g(t)j is given by:

∫[f(t)i + g(t)j]dt = [∫f(t)dt]i + [∫g(t)]j

The definite integral of a vector-valued function is:

2. The indefinite integral of a vector-valued function r(t) = f(t)i + g(t)j + h(t)k is given by:

∫[f(t)i + g(t)j + h(t)j] = [∫f(t)]i + [∫g(t)]j + [∫h(t)]k

The definite integral of a vector-valued function is:

Examples

Calculate each of the following integrals:

Solution

a. Let's use the first part of the definition of the integral of a space curve:

Practice

Calculate the following integral:

Tangent vector and unit tangent vector

 Goal:

1. Define tangent vector and unit tangent vector

Tangent vector and unit tangent vector

Let's remind that the derivative of a function at a point is the slope of the tangent line to the graph of this function at this point. In the case of a vector-valued function the derivative provides a tangent vector to the graph of this function.

Let's consider a vector-valued function and see what a tangent vector looks like on its graph. We have the vector-valued function r(t) = sinti + costj . Its derivative is r'(t) = costi-sintj. Let's substitute t = π/6 in both functions: 

Here is the graph of the function with the vectors r(π/6) r'(π/6):

Notice that the the tangent vector r'(π/6) is tangent to the circle at the corresponding point t =  π/6. This is an example of the tangent vector to the plane curve defined by the function r(t) = sinti + costj

Definition

Let C be a curve defined by a vector-valued function r, and assume that r'(t) exists when t = t₀. A tangent vector v at t = t₀.is any vector such that, when the tail of the vector is placed at point r(t₀) on the graph, vector v is tangent to curve C. Vector r'(t₀) is an example of a tangent vector at point t =  t₀.. Furthermore, assume that r'(t) ≠ 0. The principal unit tangent vector at t is defined to be:

 

The unit tangent vector is exactly what it sounds like: a unit vector that is tangent to the curve. To calculate a unit tangent vector, find the derivative r'(t). Second, calculate the magnitude of the derivative. The third step is to divide the derivative by its magnitude.

Example

Solution

Practice

Properties of the derivatives of vector-valued functions

 Goal: Calculate the derivatives of vector-valued functions using the properties of derivatives

Properties of the derivatives of vector-valued functions

The constant multiple rule, the sum and difference rule, the product rule and the chain rule used in real valued functions are also applicable for vector-valued functions.

Theorem

Let r and u be differentiable vector-valued functions of t. Let f be a differentiable real-valued function of t and c a scalar.

In property IV, we use dot product and in property V cross product.

Example:

Calculate each of the derivatives using the properties of the derivatives of vector-valued functions.

Solution

a.

According to property IV (dot product), we have:

b. To solve this problem, we need to adapt it to property V (cross product). Property V is stated as follow:

Recall that the cross product of any vector with itself is zero. Let's calculate the second derivative of u(t):

Finally we have:

Practice

Differentiation of vector-valued functions

Goal: Find the derivative of vector-valued functions by calculating the derivative of the real-valued functions of the vector-valued function.

Differentiation of vector-valued functions

Let's consider the vector-valued function r(t) = f(t)i + g(t)j or r(t) = f(t)i + g(t)j + h(t)k, we can find the derivative of these vector-valued  functions by calculating the derivative of the real-valued functions . The following theorem allows us to do that.

Theorem

Let f, g, h be differentiable functions of t:

Example

Use differentiation to find the derivative of the following vector-valued functions:

Solution

Let's use the formula of the differentiation of vector-valued functions and the formulas of the differentiation of real-valued functions

Practice

Calculate the derivative of the following function:

Derivative of vector-valued functions

 Objective: Define the derivative of a vector-valued function

Since the limit of a vector-valued function has been defined, we can now define its derivative. The definition of the derivative of a vector-valued is similar to that of real-valued functions. The only difference is in the range of the derivative of vector-valued functions. Since the range of a vector-valued function is made of vectors, the range of the derivative of the vector-valued function consists also of vectors. 

Definition

The derivative of a vector-valued is defined by:

provided that the limit exists. If r'(t) exists, then r is differentiable at t. If r is differentiable for all values of t in an open interval (a, b), then r is differentiable in this interval. The following two limits'  must exist as well for the function r to be differentiable in a closed interval [a, b]. 

and

Example

Solution

Let's apply the formula:

Practice

Use the definition to find the derivative of the vector-valued function:

Limit of a vector-valued function

 Goal: Determine the limit of a vector-valued function

Definition

This is a rigorous definition. In practice we apply the following theorem:

Theorem

Limit of a vector-valued function

Let f, g, h be functions of t and r(t) = f(t)i + g(t)j, the limit of r as t approaches a is defined by:

Similarly, the limit of the vector-valued function r(t) = f(t)i + g(t)j + h(t)k as t approaches a is defined by:

Examples

For each of the vector-valued functions calculate lim r(t) when t approaches 3:

a. r(t) = (t²- 3t + 4)i + (4t + 3)j

b. r(t) = (2t-4/t+1)i + (t/t²+1)j + (4t - 3)k

Solution

a. Using the definition of limit above and substituting t, we have:

 

b. Doing the same:

Practice

Calculate limr(t) when t approaches 2 for:

Graph of a vector-valued function

Goal:  Graph of a vector-valued function

Considerations

A vector is defined by two quantities: magnitude and direction. If we consider an initial point and move in a certain direction according to a certain distance, we arrive at a second point. The second point is the terminal point. To determine the coordinates of a vector, we subtract the coordinates of the original point from those of the terminal point.

A vector is said to be in standard position if if its original point is located in the origin. In order to maintain the uniqueness of the graph of a vector-valued function, we start by graphing the vectors in the domain of the function.. The graph of a vector-valued function of the form r(t) = f(t)i + g(t)j is the sets of all (t, r(t)) and the path it traces is called a plane curve. The graph of a vector-valued function of the form r(t) = f(t)i + g(t)j + h(t)k and the path it traces is called a space curve. Any representation of a plane curve or space curve using a vector-valued function is called a vector parameterization of the curve.  

Examples

Create  a graph of each of the vector-valued functions:

a. The plane curve represented by r(t) = 4costi + 3sintj 0 ≤ t ≤ 2ℼ

b. The plane curve represented by r(t) = 4costi + 3sintj 0 ≤ t ≤ π

Solutions

a. We start by creating a table of values made of values of t in the domain of the vector valued-function and corresponding values of r(t). We graph each of the vectors of the second column in standard form and connect the terminal point of each vector to form a curve. It turns out that the curve is an ellipse centered at the origin 

Graph

b. Let's do the same for the same for the second example.

Table of values

Graph

The graph of this curve is an also an ellipse centered at the origin.

Practice

Create of the vector-valued function: