Goal: Determine the limit of a vector-valued function
Definition
This is a rigorous definition. In practice we apply the following theorem:
Theorem
Limit of a vector-valued function
Let f, g, h be functions of t and r(t) = f(t)i + g(t)j, the limit of r as t approaches a is defined by:
Examples
For each of the vector-valued functions calculate lim r(t) when t approaches 3:
a. r(t) = (t²- 3t + 4)i + (4t + 3)j
b. r(t) = (2t-4/t+1)i + (t/t²+1)j + (4t - 3)k
Solution
a. Using the definition of limit above and substituting t, we have:
b. Doing the same:
Practice
Calculate limr(t) when t approaches 2 for:



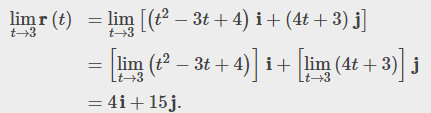

No comments:
Post a Comment