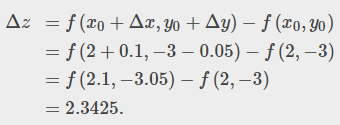Chain rule of a function of two variables x and y where x and y are function of two independent variables

 Goal: Calculate the derivation of a function of two variables x and y where x and y are functions of two independent variables.

Let's recall earlier when x and y are function of one variable, the formula is a sum of 2 products of derivatives. where z is differentiated partially with respect to x and y. Then x and y are differentiated normally with respect to the independent variable. To recall the formula easily, let's start by writing the first term of each of the 2 products. These first terms are respectively the partial derivatives of z with respect to x and with respect to y. Let's start as follows;

dz/dx = ẟz/ẟx ..... + ẟz/ẟy......

Now complete the first and the second product. The term that completes the first product is the regular derivative of x with respect to the independent variable (t). The term that completes the second product is the regular derivative of y with respect to the independent variable (t). Then we have:

dz/dx = ẟz/ẟx.dx/dt + ẟz/ẟy.dy/dt

Chain rule for a function of two independent variables

The expressions in these formulas are going to be in partial derivatives only.. We have a function of two variables z = f(x, y) where x and y are functions of two independent variables: x = x(u,v) and y = (u, v). We are going to have 2 expressions of partial derivatives. One expression of partial derivative  of z with respect to u and  another expression with respect to v. In the first expression we derive with respect to u and in the second we derive with respect to v. Each expression of partial derivative is a sum of products of derivatives as for the derivative for one variable.

Let's start with the partial derivative with respect to u. In this expression we derive x and y partially with respect to to u. Let's start by writing the first term of each product: they are partial derivative of z with respect to x and y.  We have:

 ẟz/ẟu =  ẟz/ẟx ....+   ẟz/ẟy....

Let's complete each product by deriving x partially with respect  to u in the first product and y partially with respect to u in the second product

ẟz/ẟu =  ẟz/ẟx.ẟx/ẟu +   ẟz/ẟy.ẟyẟu.

Let's write the expression of ẟz/ẟv  . We follow the same procedure by writing the first terms of each product.

 ẟz/ẟv =  ẟz/ẟx ....+   ẟz/ẟy....

Let's complete the second terms of the products by differentiating x and y partially with respect to v.

ẟz/ẟu =  ẟz/ẟx.ẟx/ẟv. +   ẟz/ẟy.ẟx/ẟv.

Theorem. Chain rule for two independent variables

Suppose x = (u, v) and y = (u, v) are differentiable functions of u and v and z = f(x, y) is a differentiable function of x and y. Then z = f((u,v), (u,v)) is differentiable of u and v. We have the following formulas:

and

Example

Solution

Let's apply the first formula:

 

Let's calculate the partial derivatives:

Let's substitute everything in the formula. We have:

Let's substitute x and u:

Let's now use the second formula, First let's calculate ẟx/ẟv and ẟ/ẟv:

We need to calculate the missing terms ẟx/ẟv and ẟ/ẟv:

Let's substitute the partial derivatives:

Let's substitute x and y:

Practice

and

 

Chain rule of a function of two variables for one independent variable

 Goal: State the chain rule for one independent variable

Chain rule for one independent variable

In a function of one variable, one of the most useful rules of differentiation is the chain rule. The same concept is applied for the differentiation of functions of more than one variable.

Recall that the chain rule for a function of one variable is given by:

In this equation both f(x) and g(x) are functions of one variable. Let's suppose that f is a function of two variables and g a function of one variable, then the derivative of of the composition of the two functions is given by the following theorem:

Theorem

Let's suppose that x = g(t) and y = h(t) are two differentiable functions of t and z = f(x,y) a differentiable function of x and y, then z = (x(t), y(t)) is a differentiable function of t and

where the ordinary derivatives are evaluated at t and the partial derivatives at (x,y).

Example

Calculate dz/dt for each of the following functions:

Solution

a.  In order to use the chain rule, let's calculate:

We have:

Let's substitute these quantities in the formula that allows to calculate dz/dt

b. Let's calculate the 4quantities representing the partial derivatives and the ordinary derivatives in order to apply the chain rule:

Let's substitute these quantities in the formula of the chain rule:

Let's substitute  eܑ^-t by 1/e^t  we have:

dz/dt = 2 e^6t +1 / e^t⎷e^6t - 1

The same result can be obtained by substituting x(t) and y(t) into z = f(x, y) and then differentiating with respect to t:

Let''s differentiate using the chain rule for a function of a single variable:

Practice

Calculate dz/dt given the following functions:

Express the final answer in terms of t.

Notion of differential of a function of two variables

 Notions of differentials

In linear approximation and differentials for a function of one variable, the differential of y written as dy is defined as f'(x)dx. The differential is used to approximate Δy = f(x + Δx) - f(x) where  Δx = dx. Extending this notion to the linear approximation of a function of two variables at the point (x₀, y₀)  leads to the concept of total differential of a function of two variables.

Definition

Let z = f(x,y) be a function of two variables with (x₀, y₀) and (x₀ + Δx , y₀ + Δy) both in the domain of f. If f is differentiable at the point (x₀, y₀) , then the differentials for dy and dx are written as dx = Δx and dy = Δy.

The differential dz called total differential of z = f(x,y) is given by:

dz = fₓ(x₀, y₀)dx + f y(x₀, y₀)dy.

This formula can be used to approximate Δz as shown in the following example:

Example

Find the differential dz of the function f(x, y) = 3x ²- 2xy + y² and use it to approximate Δz at the point (2, -3). Use Δx = 0.1 and Δy = -0.05. What is the exact value of Δz ?

Solution

Let's use the formula:  dz = fₓ(x₀, y₀)dx + f y(x₀, y₀)dy

Let's substitute  (x₀, y₀) :

 dz = fₓ(2, -3)dx + f y(2, -3)dy

Let's calculate fₓ(2, -3 and  f y(2, -3:

fₓ (x, y) = 6x -2y  

fₓ(2, -3 = 6(2) - 2(-3) = 12 + 6 = 18

fy(x, y) = -2x + 2y

 f y(2, -3) = -2(2) + 2(-3) =  -4 - 6 = -10.

Let's substitute  fₓ(2, -3) dx, f y(2, -3) dy in the formula of the total differential:

dz = 18(0.1) - 10(-0.05) = 2.3

The exact value of Δz is given by:

Practice

Find the differential of the function:

and use it to approximate Δz au point (1, -1). Use   Δx = 0.03 and Δy = -0.02. What is the exact value of Δz ?
 

Linear approximations for functions of two variables

 Goal: Use the tangent line to approximate a function of two variables at a point.

Linear approximations

Let's recall that the linear approximation for a function of one variable f(x) at a point x = a  is given by:

Here is the diagram of the linear approximation of a function of one variable:

When we look at the diagram, for values close to x = a., the tangent line is confounded with the curve of the function represented by y =f(x).

The tangent line can be used as an approximation to the function y = f(x) for values of x reasonably close to x = a. 

The concept is the same for a function of two variables. The tangent line is replaced by the tangent plane.

Definition

Given the function  z = f(x, y) with partial derivatives at the point (x₀, yₒ), the linear approximation of at the point (x₀, yₒ) is given by the equation:

We can notice that this equation represents the tangent line to the surface z = f(x,y) at the point  (x₀, yₒ). It holds all the points (f(x,y) , (x,y)) close to (f(x₀, y₀), (x₀,y₀)) for values of (x,y) close to (x₀,y₀).

Exemple

Given the function: 

Approximate the point f(2.1, 2.9) using the point (2, 3) for (x₀, y₀). What is the approximate value of 

f(2.1, 2.9 to 4 decimal places.

Solution

Let's apply the formula of the equation of the linear approximation:

Let's calculate f(x₀, y₀), fₓ(x₀, y₀), fy(x₀, y₀) for x₀ = 2 and y₀ = 3.

Let's substitute all the elements in the equation of the linear approximation above:

L(x, y) = 4 - 2(x - 2) - 3/4(y - 3)

Let's substitute x =2.1 and y = 2.9 into L(x, y):

The approximate value of f(2.1, 2.9) to 4 decimal places is:

This corresponds to an error of approximation of 0.2%.

Practice

Given the function 

Approximate f(4.1, 0.9)  using the point (4, 1) for (x₀, y₀). What is the approximation of f(4.1, 0.9) using 4 decimal places?

Tangent plane to a surface at a point

 Goal: Determine the equation of a plane tangent to a surface at a point.

Tangent plane

In a two-dimensional space only one line can be tangent to a curve at a point  However, in a three-dimensional space many lines can be tangent to a curve at a point. A tangent plane is a plane made of all the tangent lines to a curve at a point. When a plane is tangent to a surface at a point, that surface is smooth there meaning there are no corners or discontinuities at that point. A tangent line to the surface at that point  in any direction doesn't have any abrupt changes in slope because the direction changes smoothly.

Definition

Let P₀ = (x₀, y₀, z₀) bee a point at a surface S, and let C be any curve passing by P and lying entirely on S, if the tangent lines to all such curves  C at P₀ lie in the same plane, then the plane is called the tangent plane to S at P₀

Tangent plane

In order for a tangent plane to a surface at a given point to exist, the function that defines the surface has to be differentiable at that point.

Definition

Let S be a surface defined by a differentiable function z = f(x. y) and let P₀ = (x₀, y₀) a point in the domain of. Then, the equation the equation of the tangent plane to S at P₀ is defined by:

Example

Find the equation of the tangent line to the surface defined by the equation:

Solution

Let's calculate f(2, -1):

Let's calculate the partial derivatives with respect to x and y respectively:

Let's calculate the partial derivatives with respect to x and y for the point (2, -1):

LFet's substitute all the elements in the equation of the tangent plane given above:

Figure

Practice

Find the equation of the  tangent plane to the surface defined by the equation: