Notions of differentials
In linear approximation and differentials for a function of one variable, the differential of y written as dy is defined as f'(x)dx. The differential is used to approximate Δy = f(x + Δx) - f(x) where Δx = dx. Extending this notion to the linear approximation of a function of two variables at the point (x₀, y₀) leads to the concept of total differential of a function of two variables.
Definition
Let z = f(x,y) be a function of two variables with (x₀, y₀) and (x₀ + Δx , y₀ + Δy) both in the domain of f. If f is differentiable at the point (x₀, y₀) , then the differentials for dy and dx are written as dx = Δx and dy = Δy.
The differential dz called total differential of z = f(x,y) is given by:
dz = fₓ(x₀, y₀)dx + f y(x₀, y₀)dy.
This formula can be used to approximate Δz as shown in the following example:
Example
Find the differential dz of the function f(x, y) = 3x ²- 2xy + y² and use it to approximate Δz at the point (2, -3). Use Δx = 0.1 and Δy = -0.05. What is the exact value of Δz ?
Solution
Let's use the formula: dz = fₓ(x₀, y₀)dx + f y(x₀, y₀)dy
Let's substitute (x₀, y₀) :
dz = fₓ(2, -3)dx + f y(2, -3)dy
Let's calculate fₓ(2, -3 and f y(2, -3:
fₓ (x, y) = 6x -2y
fₓ(2, -3 = 6(2) - 2(-3) = 12 + 6 = 18
fy(x, y) = -2x + 2y
f y(2, -3) = -2(2) + 2(-3) = -4 - 6 = -10.
Let's substitute fₓ(2, -3) dx, f y(2, -3) dy in the formula of the total differential:
dz = 18(0.1) - 10(-0.05) = 2.3
The exact value of Δz is given by:
Practice
Find the differential of the function:
and use it to approximate Δz au point (1, -1). Use Δx = 0.03 and Δy = -0.02. What is the exact value of Δz ?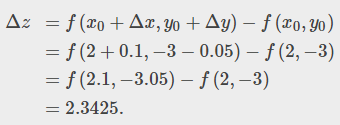
No comments:
Post a Comment