Objective: Convert the parametric equations of a curve into the form y = f(x)
Conversion of the parametric equations of a curve into an explicit form
Usually we are more accustomed in graphing the curve of a function represented explicitly meaning representing a relation between y and x. It is possible to convert the parametric equations of a curve into its explicit form. The process is very simple. It consist in finding the expression of t in one of the parametric equations and then substituting it in the other.
Examples:
a) let's solve example a)
Let's find t in the first equation. We can also find it in the second equation.
Let's substitute t in the second equation:
This is the equation of a parabola opening upward. The limits of the parameter lead to a domain restriction of the function.
The interval for t is mentioned in the problem: -6≤t≤-2
Let's substitute t = -6 in the expression of x, we find x = 0. Let's substitute t = -2 in the expression of x, we find x = 4. The domain of the function is D = [0,4].
b) I am not going to solve completely the example 2. I'll give some steps.
Instead of solving for t find sint and cost in both equations. Substitute sint and cost in the identity sin²t + cos²t = 1. The equation found is the equation of an ellipse centered in the origin.
Practice
Eliminate the parameter for the plane curve defined by the following parametric equations and describe the resulting graph:
x(t) = 2 + 3/t y(t) = t-1 2≤t≤6
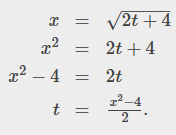


No comments:
Post a Comment