In the previous post, we set the formula to find the area of a region bounded by a polar curve. Let's do an application.
Example. Find the area of one petal of the rose defined by the equation r = 3sin (2θ)
Solution
Here is the graph of the of the petal of the rose
The first petal of the rose is traced out from the polar coordinates (0, 0) and (0, 𝝅/2). To find the area inside the petal, let's use the formula of the area of the region bounded by a polar curve. In this formula we substitute 𝛼 by 0 and 𝛽 by 𝝅/2.
To evaluate this integral, let's use the formula sin²𝛂 = 1 - cos(2𝛂) with 𝛂 = 2𝜃
Practice
Find the area inside the cardioid defined by the equation r = 1-cos𝜃

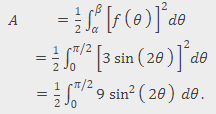

No comments:
Post a Comment