Goals:
1) Define polar coordinates
2) Convert points between rectangular and polar coordinates
Polar Coordinates
Definition
The rectangular coordinate system provides a way to map points to ordered pairs. The polar coordinate system provides an alternative method for mapping points to ordered pairs.
Let's consider the following figure:
The point P has has (x,y) for coordinates in the rectangular coordinate system. The line segment that joins the origin to the point P measures the distance between these two points. This distance is designated by the letter r.. The angle between this segment and the positive part of the x-axis is designated by Ө. Now the point P can not only be referred by its cartesian coordinate x and y but by r and Ө. These 2 letters represent the polar coordinates of the point P.
Converting points between coordinate systems
Theorem
Given a point P in the plane represented by its cartesian coordinates (x,y) and its polar coordinates (r,θ), the following relations hold true:
These formulas can be used to convert from cartesian coordinates to polar coordinates and vice-versa.,
Examples
Converting between rectangular and polar coordinates
1. Convert each of the following points into the polar coordinate system:
2. Convert each of the following points into the rectangular coordinate system:
Solution
1.
Practice





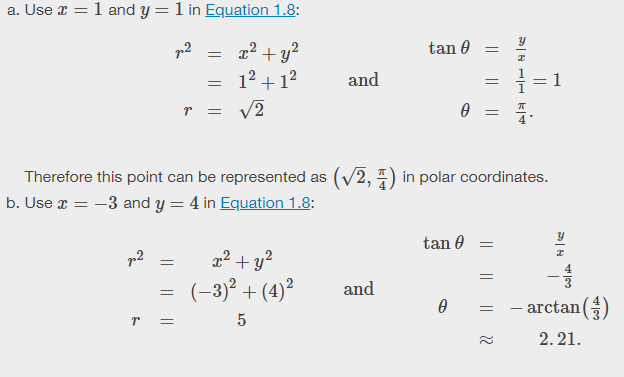

No comments:
Post a Comment